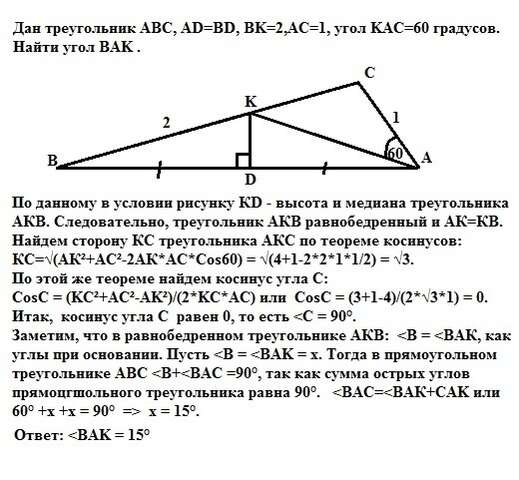
По данному в условии рисунку КD - высота и медиана треугольника АКВ. Следовательно, треугольник АКВ равнобедренный и АК=КВ. Найдем сторону КС треугольника АКС по теореме косинусов: КС=√(АК²+АС²-2АК*АС*Cos60) = √(4+1-2*2*1*1/2) = √3.
По этой же теореме найдем косинус угла С:
CosC = (KC²+AC²-AK²)/(2*KC*AC) или CosC = (3+1-4)/(2*√3*1) = 0. Итак, косинус угла С равен 0, то есть
Заметим, что в равнобедренном треугольнике АКВ: x = 15°.
Ответ: