ДАНО:
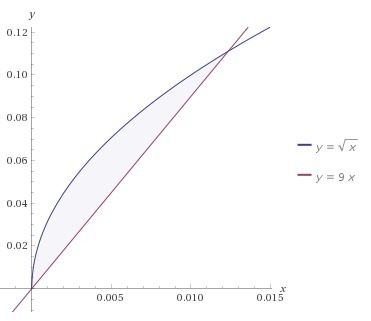
y(x) = √x = x¹/² и f(x) = 9*x
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
Находим пределы интегрирования решив равенство y(x) = f(x).
x¹/² = 9*x, x = 81*x²
a = 1/81 - верхний предел , b = 0 - нижний предел,
Находим разность функций - функция y(x) выше, чем функция f(x)
s(x) = x¹/² - 9*x - исходная функция площади - интегрируем.
![S(x)=\int\limits^a_b {(\sqrt{x}-9 x)} \, dx=\frac{2}{3}\sqrt[3]{x^2}-\frac{9x^2}{2}](https://tex.z-dn.net/?f=S%28x%29%3D%5Cint%5Climits%5Ea_b%20%7B%28%5Csqrt%7Bx%7D-9%20x%29%7D%20%5C%2C%20dx%3D%5Cfrac%7B2%7D%7B3%7D%5Csqrt%5B3%5D%7Bx%5E2%7D-%5Cfrac%7B9x%5E2%7D%7B2%7D "S(x)=\int\limits^a_b {(\sqrt{x}-9 x)} \, dx=\frac{2}{3}\sqrt[3]{x^2}-\frac{9x^2}{2}")
Вычисляем, подставляя верхний предел - а. S(0)=0,
S(a) = 1/4374 - площадь - ОТВЕТ.
Рисунок к задаче в приложении.
