(2)
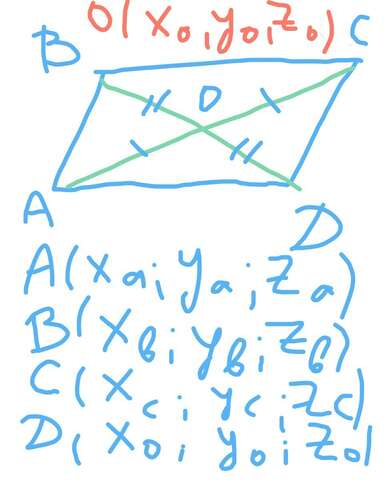
точка пересечения диагоналей
параллелограмма делит их пополам
АО=ОС
BO=BD
найдем координату точки О,
середины АС

но точка О является и серединой BD
поэтому

(x_d, y_d, z_d)) = \\ = 2(x_o, y_o, z_o) - (x_b, y_b, z_b) = \\ = (2x_o - x_b,2y_o - y_b, 2z_o-z_b) = \\ = ( - 1,4,14)" alt="(x_o, y_o, z_o) = \\ = \frac{1}{2} ((x_b, y_b, z_b) + (x_d, y_d, z_d)) \\ = > (x_d, y_d, z_d)) = \\ = 2(x_o, y_o, z_o) - (x_b, y_b, z_b) = \\ = (2x_o - x_b,2y_o - y_b, 2z_o-z_b) = \\ = ( - 1,4,14)" align="absmiddle" class="latex-formula">