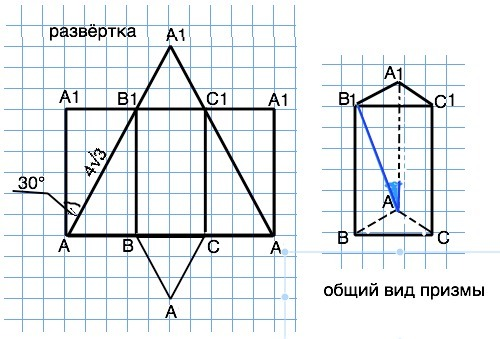
Диагональ боковой грани правильной треугольной призмы равна 4√3 и составляет с ребром основания угол 30°. Нужно найти площадь полной поверхности призмы. Назовём призму АВСА1В1С1. Диагональ АВ1=4√4,
Площадь полной поверхности призмы равна сумме площадей боковой поверхности и двух оснований.
В прямоугольном ∆ АА1В1 катет А1В1 противолежит углу 30° и равен половине длины гипотенузы АВ1 (свойство). А1В1=2√3. Высота призмы АА1=А1В1•tg60°=2√3•√3=6. Ѕ(бок)=a•h=3•A1B1•AA1. По формуле площади правильного треугольника площадь двух оснований 2•S(осн)=((A1B1)²•√3)/4 Площадь полной поверхности призмы:
Ѕ(полн)=Ѕ(бок)+Ѕ(осн)=3•(6•2√3)+2•(2√3)²•√3:4=36√3+6√3=42√3 ед. площади.