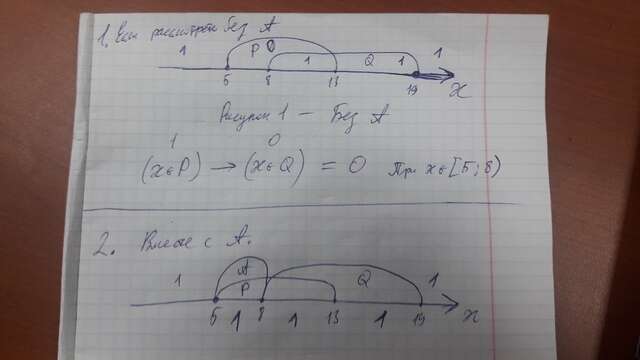
Для начала изобразим числовую прямую OX и изобразим на ней отрезки P и Q.
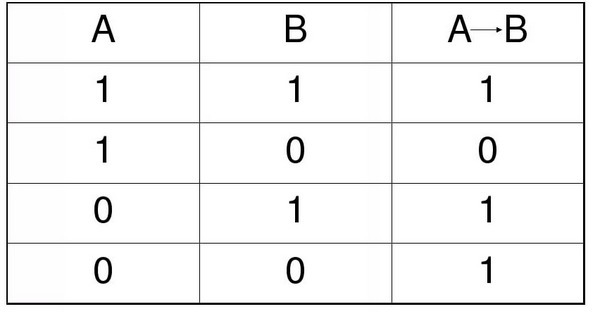
1. Рассмотрим, как ведёт себя формула, если не учитывать существование отрезка A: U1 = (x∈P) → (x∈Q) (таблица истинности для логического следования приведена на рисунке 1)
Как видно на рисунке 2.1, на луче [5;8) формула U1 принимает значение 0, а во всех остальных областях — 1. Это происходит из-за того, что на этом луче возникает случай (1) → (0).
Таким образом, добавление отрезка А на ось OX должно избалвять нас от вышеуказанного случая. Вариантов избавления 2: свести к (0) → (0) или свести (1) → (1).
Первый варинат: (x∈P)∧¬(x∈А) = 0. Так как мы по условию находимся в [5;8), то (x∈P) = 1 и таким образом 1∧¬(x∈А) = 0, то есть ¬(x∈А) = 0. Значит x∈А = 1 и А должен быть = [5;8). Точка 8 входит ещё и в Q. Если её проверить, то и она подойдет. То есть [5;8]. Длина отрезка = 3.
Второй вариант: (x∈Q)∧¬(x∈А) = 1. Напомню, что по условию, мы находимся в [5;8), где (x∈Q) = 0, то есть не зависимо от выбора отрезка А, (x∈Q)∧¬(x∈А) = 0. То есть этот вариант не подходит.
Так методом исключения мы оставили один единственный вариант А = [5;8]. Проверим, не изменило ли добавление А истинность формулы на других участках. (рисунок 2.2)
Ответ: минимальная длина отрезка А = 3.