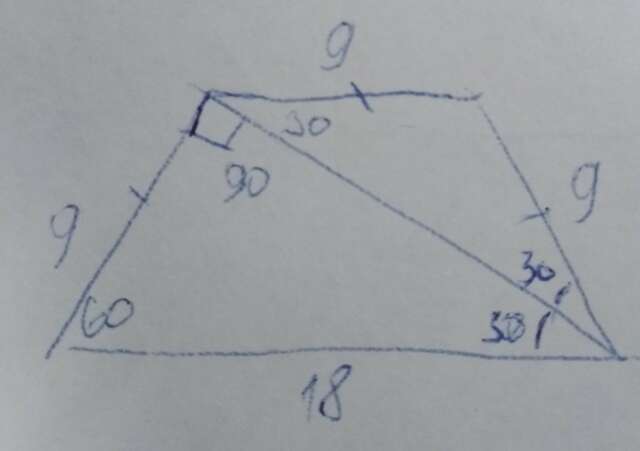
Если диагональ является биссектрисой, то она является катетом прямоугольного треугольника с гипотенузой из большего основания трапеции. И меньший катет мы находим через Sin половины угла при основании. Почему прямоугольный? Поэтому-что у нас есть два угла 60 и 30, а сумма всех углов треугольника равна 180.
Соответственно боковая грань будет равна 18*Sin30°=9.
Второй же теугольник у нас получается равнобедренный. Т.к. тупые углы в трапеции равны (360-2*60)/2=120°, а 90° из 120 отъел первый треугольник. У нас получился треугольник с углами по 30° при основании и 120° в вершине. А если он равнобедренный, то и его стороны при равных углах равны, получаем, что верхнее основание равно 9, а периметр будет 9+9+9+18=45