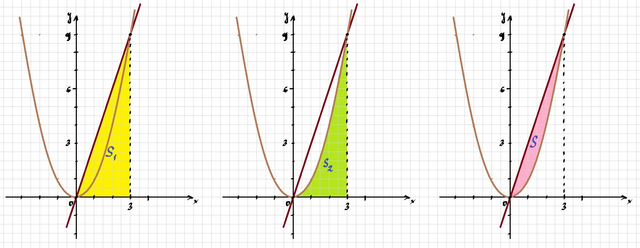
Найдем точки, в которых графики этих функций пересекаются (расположение графиков функций смотри на рисунке). Для этого решим систему уравнений:

Вычтем из первого уравнения второе:

Найдем площадь фигуры, ограниченной функцией у=3х, осью Ох и прямыми х=0, х=3.

Найдем пощадь фигуры, ограниченной функцией  , осью Ох и прямыми х=0, х=3.
, осью Ох и прямыми х=0, х=3.

Теперь из первой площади вычтем вторую и получим искомую величину.

Ответ: S=4,5.