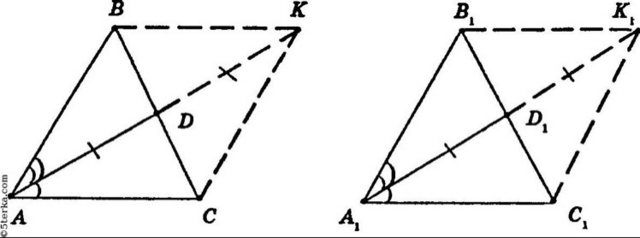
DK = AD(на рисунке видно)
Продолжим A1D1 до точки K1, =>D1K1 = A1D1. ΔADC и ΔDBK=>AD = DK
∠ADC = ∠BDK (вертик) BD = DC (т.к. AD — медиана)
ΔADC = ΔDBK (по 1-му признаку равенства треугольников)=> ∠DAC = ∠DKB
Далее;
AK = A1K1 (т.к. AK = 2AD = A1K1) ∠BAK = ∠B1A1K1 (по рисунку )
∠BKA = ∠B1K1A1 (т.к. ∠BKA = ∠KAC = ∠K1A1C1 = ∠B1K1A1)
Значит ΔABK = ΔA1B1K1 (по 2-му признаку равенства треугольников)=>АВ = А1В1, и BK = B1K1 = А1С1 = АС.
∠ВAС = ∠В1A1С1=>ΔАВС = ΔA1В1С1. A1B1K1 (по 1-му признаку равенства треугольников.)