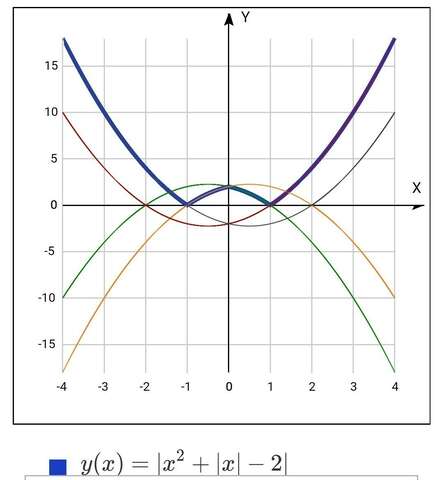
так как

то

функция чётная
функция определена для всех х
Dy:x€R
Еу:[0,+∞)
то есть функция ограничена , она принимает только неотрицательные значения (из-за свойств модуля)
и принимает вид:

каждый из этих промежутков
разбивается ещё на два (см фото)
при x≥0
x²+x-2≥0
(x-1)(x+2)≥0
[0,1)v[1;+∞)
при x<0<br>х²-х-2≥0
(х-2)(х+1)≥0
(-∞;-1]v(-1;0)
функция будет иметь следующий вид
на этих промежутках

x \geqslant 0) = - ({x}^{2} + x - 2)}} \right. } \atop {\left \{ {{(0 > x \geqslant - 1)= {x}^{2} - x - 2} \atop {( - 1 > x ) = - ({x}^{2} - x - 2)}} \right.}} \right. \\ " alt="y(x) = \left \{ {{\left \{ {{(x \geqslant 1) = {x}^{2} + x - 2} \atop {(1 > x \geqslant 0) = - ({x}^{2} + x - 2)}} \right. } \atop {\left \{ {{(0 > x \geqslant - 1)= {x}^{2} - x - 2} \atop {( - 1 > x ) = - ({x}^{2} - x - 2)}} \right.}} \right. \\ " align="absmiddle" class="latex-formula">
у(х)=|f(x)|≥0, поэтому
решим у(х)=0

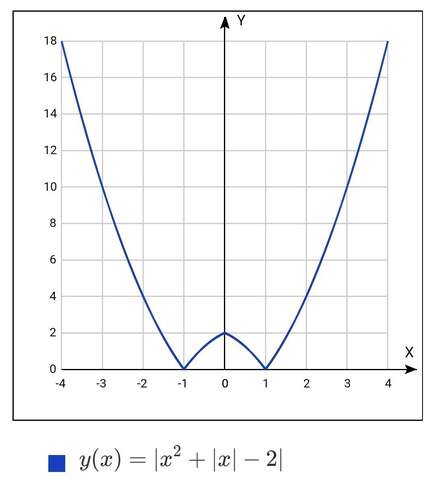
при х¹'²=±1 ( кстати, это нули функции), функция примет наименьшее значение =0
yнаибольшее =+∞
график на рисунке