Для начала составим уравнения перемещения:
S0 = (V0+V1)*t0
S1 = V1*(t0+4)
По условию: S0 = S1
Значит:
(V0+V1)*t0 = V1*(t0+4) = V1*t0+4V1
(V0+V1)*t0 - V1*t0 = V0*t0 = 4V1
t0 = 4*V1÷V0
Так как движутся в одном напралвении: V0 > 0
Отсюда видно, что зависимость обратно пропорциональная. И так как ограничения на скорость V0 в условии не задано, то можно подобрать скольугодно большую скорость, такую, что время t0 будет < 2.
Проверим в табличном процессоре.
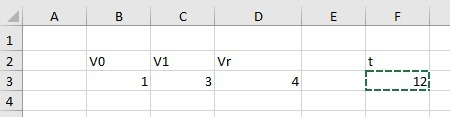
Создадим документ со следующей структурой (рисунок 1).
Выставим V1 согласно условиям. V0 изначально пусть будет = 1. (рисунок 2)
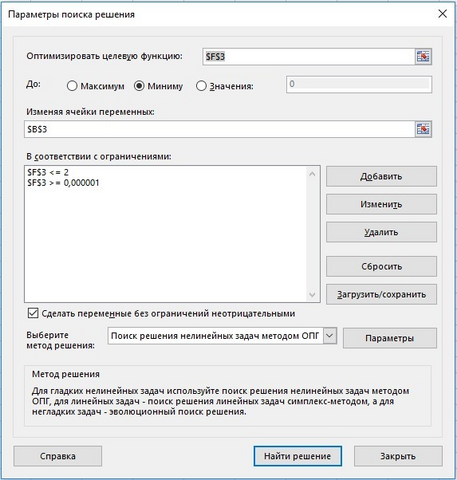
Проведём поиск решений, оптимизируя время и изменяя скорость V0, со следующими ограничениями (рисунок 3)
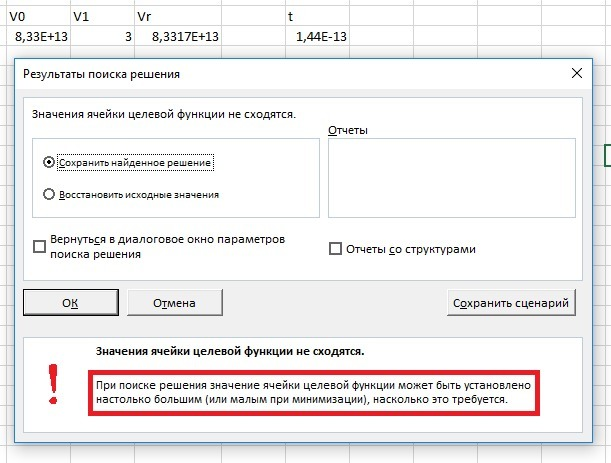
В результате табличный процессор сообщает, что время может быть сколь угодно маленьким. (рисунок 4).