Дан треугольник со сторонами 6, 8, 10 . найдите синус наименьшего угла этого треугольника

Question

Дан треугольник со сторонами 6, 8, 10 . найдите синус наименьшего угла этого треугольника

Answer 1

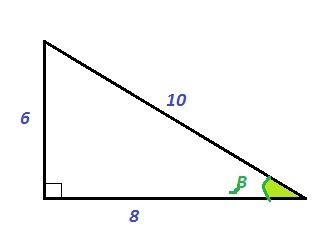
В любом треугольнике напротив меньшего угла расположена меньшая сторона. Значит, наименьшим будет угол напротив стороны 6, между сторонами  8 и 10.

Вид данного треугольника :

6² + 8² = 36 + 64 = 100 = 10²

Справедлива теорема Пифагора, значит, треугольник - прямоугольный. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе :

---

Answer 2

Против меньшей стороны - наименьший угол. Также заметим, что треугольник со сторонами 6, 8, 10 является прямоугольным. Это можно показать, используя теорему Пифагора

6² + 8² = 10²

Синус - отношение противолежащего катета к гипотенузе

sin α = 6/10