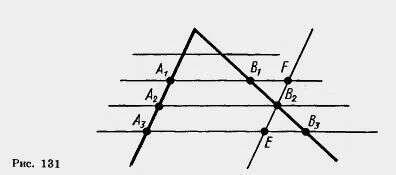
Пусть А1, А2, А3 — точки пересечения параллельных прямых с одной из сторон угла и А2 лежит между А1 и А3 (рис. 131). Пусть В1, В2, В3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если А1А2 = А2Аз, то В1В2=В2В3.
Проведем через точку В2 прямую EF, параллельную прямой A1A3. По свойству параллелограмма A1A2=FB2, А2А3 = B2E. И так как А1А2=А2А3, то FВ2=В2Е.
Треугольники B2B1F и В2В3Е равны по второму признаку. У них B2F=B2E по доказанному. Углы при вершине В2 равны как вертикальные, а углы B2FB1 и В2ЕВ3 равны как внутренние накрест лежащие при параллельных A1B1 и А3В3 и секущей EF.
Из равенства треугольников следует равенство сторон: В1В2=В2В3.