Тригонометрия плез,оч трудно

Question

Дан 1 ответ

Правильный ответ

1) Переведите радианы:

$\text{a)} \ 120^{\circ} = 120^{\circ} \ \cdotp \dfrac{\pi}{180^{\circ}} = \dfrac{2\pi}{3}$

$\text{b)} \ 243^{\circ} = 243^{\circ} \ \cdotp \dfrac{\pi}{180^{\circ}} = \dfrac{27\pi }{20}$

2) Выразите в градусах:

$\text{a)} \ \dfrac{5\pi}{12} = \dfrac{5\pi}{12} \ \cdotp \dfrac{180^{\circ}}{\pi} = 75^{\circ}$

$\text{b)} \ \dfrac{16\pi}{15} = \dfrac{16\pi}{15} \ \cdotp \dfrac{180^{\circ}}{\pi} = 192^{\circ}$

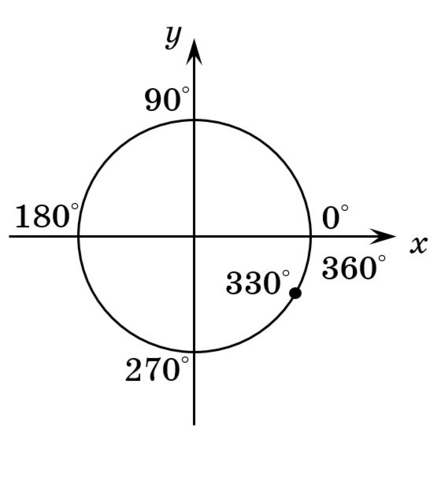
3) На числовой окружности отметьте точку с координатой:

$\text{a)} \ \dfrac{11\pi }{6} = 330^{\circ}$ (см. вложение №1)

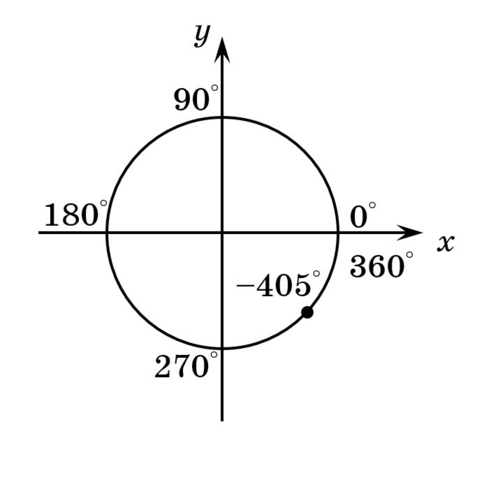
$\text{b)} \ -\dfrac{9\pi }{4} = -405^{\circ}$ (см. вложение №2)

4) В какой четверти координатной окружности лежит число:

Пояснение: чтобы узнать, в какой четверти координатной окружности лежит какое-нибудь число, надо сделать так, чтобы это число было записано в радианах (для определения четверти значение числа в радианах не обязательно должно быть точным), то есть:

$\text{a)} \ -2,7 = \dfrac{\pi}{x} \Rightarrow x = -\dfrac{\pi}{2,7} \approx -\dfrac{3,14}{2,7}\approx -1,2$ . Значит, $-\dfrac{\pi }{1,2} = -\dfrac{\pi }{\dfrac{6}{5}} = -\dfrac{5\pi}{6} = -150^{\circ} \Rightarrow -2,7 \approx 360^{\circ} - 150^{\circ} = 210^{\circ}$ - третья четверть (180° < α < 270°).

$\text{b)} \ 37 = \dfrac{\pi}{x} \Rightarrow x = \dfrac{\pi}{37} \approx \dfrac{3,14}{37}\approx 0,085$ . Значит, $\dfrac{\pi }{0,085} = \dfrac{\pi }{\dfrac{85}{1000}} = \dfrac{\pi }{\dfrac{17}{200}} = \dfrac{200\pi}{17} = \dfrac{200\pi}{17} \ \cdotp \dfrac{180^{\circ}}{\pi} \approx 37^{\circ}$ - первая четверть (0° < α < 90°).

_zn (654k баллов) 18 Май, 20