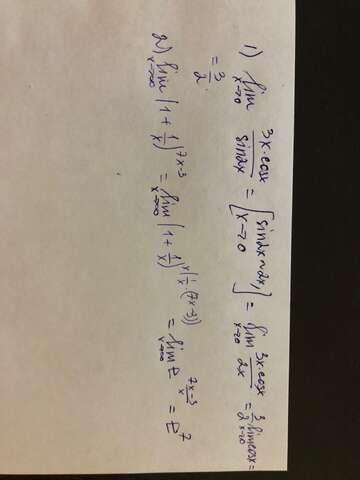Решение во вложении.
Идея:
1) Для решения понадобится знать, что такое эквивалентные функции и как они работают. В данном случае sin(2x) - функция, эквивалентная 2x при x->0, поэтому в знаменателе sin(2x) заменяем на 2x.
2) Сводим предел ко второму замечательному. Для этого показатель степени домножаем и делим на x. Применяем:

Принимая во внимание, что
 ,
,
получаем ответ: e^7.