Пожалуйста, обьясните, как это делать: Решить ГРАФИЧЕСКИ уравнение (розв'язати графічно...

$2^x + x - 1 = 0;\\2^x = 1 - x.$

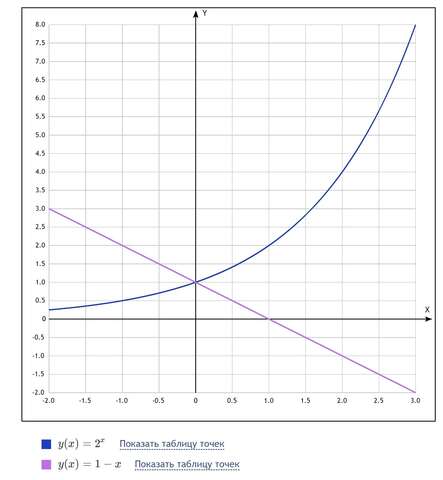
Решением уравнения будет абсцисса точки пересечения графиков функций

$f(x) = 2^x$

$g(x) = 1 - x$

Изобразим графики этих функций (во вложении график f(x) изображен синим цветом, g(x) - лиловым). По графику устанавливаем, что пересечение происходит при

$x=0.$

Таким образом, x = 0 - корень уравнения.

Ответ: 0.