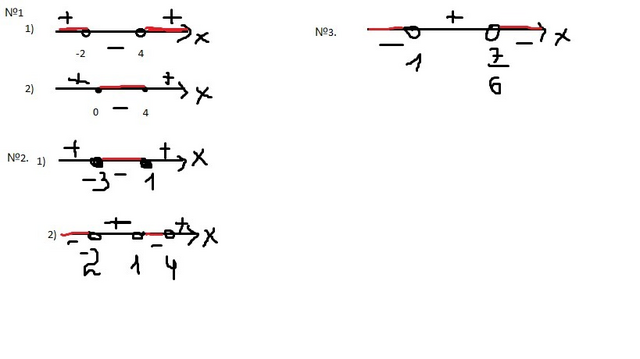
Тут всё решается методом интервалов
№1. а) x∈(-∞;-2)∪(4;+∞)
б) x∈[0;4]
№2.
а) Надо преобразовать выражение
x²+2x-3
По теореме Виета:
x1+x1=-2
x1*x2=-3
x1=1
x2=-3
x²+2x-3=(x-1)(x+3)
(x-1)(x+3)≤0
x∈[-3;1]
б) x∈(-∞;-2)∪(1;4)
№3.
Тут опять надо преобразовать.

x∈(-∞;1)∪( ;+∞)
;+∞)