Решить неравенство 1/(1+x)+2/(2+x)

$\frac{1}{1 + x} + \frac{2}{2 + x} \leqslant \frac{6}{3 + x}$
Переносим правую часть влево
$\frac{1}{1 + x} + \frac{2}{2 + x} - \frac{6}{3 + x} \leqslant 0$
Приводим к общему знаменателю
$\frac{6 + 2x + 3x + {x}^{2} + 6 + 2x + 6x + 2 {x}^{2} - 12 - 6x - 12x - { 6x}^{2} }{(1 + x)(2 + x)(3 + x)} \leqslant 0$
Находим область доп. значений
x не равен - 1
x не равен - 2
x не равен - 3

Приводим подобные
$- {3x}^{2} - 5x \leqslant 0$
Домножим обе части на - 1
${3x}^{2} + 5x \geqslant 0$
Вынесем x, Приводим кв уравнение к линейному
$x(3x + 5) \geqslant 0$
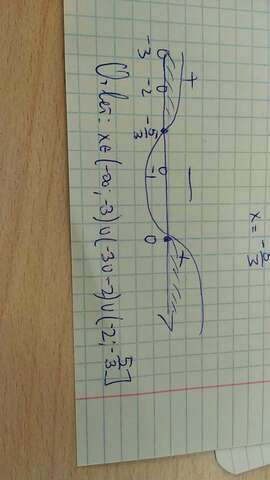
Решаем методом интервалов
Находим переломный точки, для этого приравниваем уравнение к нулю
$x(3x + 5) = 0$
Произведение равно нулю, когда один из множителей равен нулю
x=0 или x=
$- \frac{3}{5}$

Рисуем кривую знаков и находим ответ(на фото)