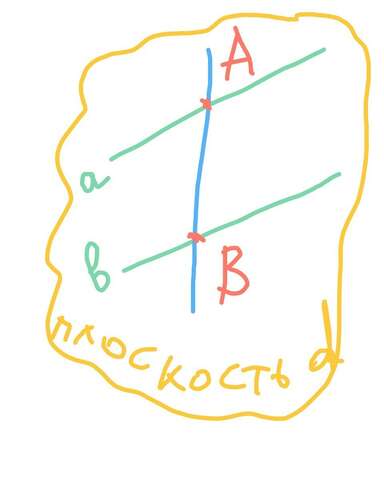
на фото
прямые
а||b
взята произвольная прямая с, которая пересекает прямые а и b в точках соответвенно А и В
итак, если прямые а и b параллельны, то через них проходит плоскость , назовем её d. ( см фото)
прямая с, которая пересекает прямые а и b,
имеет с плоскостью d две общие точки, ими будут как раз точки А и В пересечения прямой с и параллельных прямых а и b соответственно.
Но по аксиоме , если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. то есть мы получаем, что произвольная прямая с, пересекающая паралелльные а и b лежит в плоскости d.
что и требовалось доказать.