Пожалуйста постройте график функции y={x-2,если х меньше или равен 0 x^2,если х

$\displaystyle y=\begin{Bmatrix}x-2,x\ge 0\\x^2,x<0\;\;\end{matrix}$

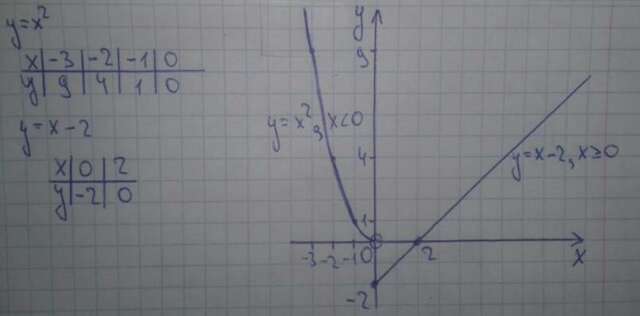
При x<0, будет график правой ветви параболы y=x², составим таблицу точек для построения. Точка (0;0) будет выколота т.к. x<0 и 0 не включается.</p>

При x≥0, будет график прямой y=x-2, найдём две точки и проведём через них прямую.

Таблицы с точками и сам график смотри в приложении.

y(3) = 3-2 = 1; вычислили через y=x-2 т.к. 3 ≥ 0.

y(0) = 0-2 = -2; т.к. 0 ≥ 0.

y(-1) = (-1)^2 = 1; т.к. -1<0.</p>

$y(a+\sqrt3 )=\begin{Bmatrix}a+\sqrt3 -2,a+\sqrt3 \ge 0\quad \\(a+\sqrt3 )^2 ,a+\sqrt3 <0\end{matrix} \\\\\boxed{y(a+\sqrt3 )=\begin{Bmatrix}a+\sqrt3 -2,a\ge -\sqrt3 \qquad \\a^2+2\sqrt3 a+3,a<-\sqrt3 \end{matrix} }$