Абстрактная функция mod принемает в класическом понимании два параметра:
Результатом этой функции будет не отприцательный остаток целочисленного деления этих чисел.
Что бы понять как работает функция, её можно представить следующим алгоритмом написанном на псевдокоде:
- function mod (integer numerator, integer denumerator)
- {
- integer wholeQuotient = numerator / denumerator;
- integer remainder = numerator - wholeQuotient;
-
- integer returnValue = 0;
-
- if (0 < remainder)
- {
- returnValue = remainder;
- }
-
- return returnValue;
- }
Описание алгоритма (номера являются номерами строк псевдокода выше):
1. Функция получает на вход два целых числа - делимое и делитель
3. Вычесляется целове частное
4. Вычисляется остаток от деления
6. Декларируется переменная что будет хранить возращяемое значение функции, по умолчанию это 0.
8. Производиться проверка, если остаток от деления не равен нулю, то:
10. Возращяемому значению функции присваевается значени остатка
13. Возращается вычисленное значение функции
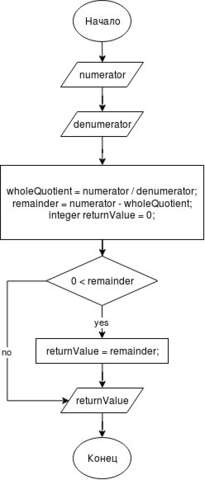
Так же прикреплена диаграма алгоритма к ответу, далее легенда диаграмы:
- Овалы - начало и конец алгоритма
- Трапеции - ввод и вывод информации
- Квадраты - выполнение неких вычеслений либо операций
- Ромбы - условия
Спасибо за отметку "лучший ответ", а также нажатую кнопочку "спасибо":
- На ответе
- В моем аккаунте
P.S.
Я описал возможный алгоритм работы функции mod, точно так же может быть реализация пошагового вычитания делителя из делимого до того момента пока делимое не станет больше делителя. Вариантов реализации может быть большое кол-во.
В случаи когда вам нужно посчитать все эти примеры, проще не решать по какому-то конкретному алгоритму, а просто делить в столбик до того момента пока у вас не останется остаток меньше делителя (но это справедливо только в отношении больших чисел, для примеров что есть у вас можно посчитать и устно).
- 2 mod 5 = 2 (2 по тому что мы пытаемся разделить 2 на 5, 5 более чем 2, следовательно целочисленно разделить невозможно и результат будет тот же что и делимое)
- 2 mod 8 = 2 (снова делитель более делимого, следовательно остаток снова равен делимому - 2)
- 2 mod 10 = 2 (такая же ситуация как и в первых двух случаях)
- 12 mod 8 - 10 mod 8 = 4 - 2 = 2(остаток от деления 12 на 8 будет 4, а остаток деления 10 на 8 будет 2, следовательно 4 - 2 = 2)
P.S.S.
Так же для оптимизации описаного мной алгоритма можно сделать условие до всяческих вычислений:
Если делитель больше чем делимое, то вернуть модуль делимого.