1.
a) 2a + 3 < 5, перенесём 3 вправо
2a < 2, поделим левое и правое выражение на 2>0
a < 1 ⇒ Ответ: a ∈ (-∞; 1)
б) 1 - b < 2b + 3, перенесём 2b влево, 1 вправо
-3b < 2, домножим обе части неравенства на (-1), знак неравенства изменится
3b > -2
b > -2/3 ⇒ Ответ: b ∈ (-2/3; +∞)
2. x²+3x+2 > 0
Независимо от неравенства приравняем уравнение к нулю и найдём корни:
x² + 3x + 2 = 0
D = b² - 4ac = 9 - 4*1*2 = 9 - 8 = 1
x₁ = (-b+√D)/2a = (-3 + 1)/2 = -1
x₂ = (-b-√D)/2a = (-3 - 1)/2 = -2
Вставляем эти корни в выражение (x - x₁)(x - x₂) = (x - (-1))(x - (-2)) = (x + 1)(x + 2), перейдём теперь к неравенству:
(x + 1)(x + 2) > 0
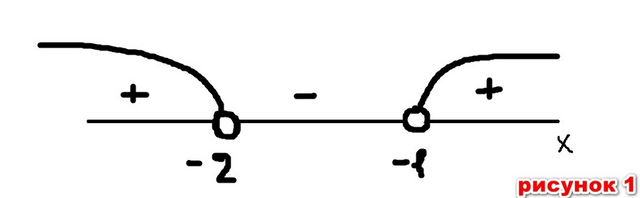
Отметим эти точки на числовой прямой (рис 1) и воспользуемся методом интервалов. Ответ: x ∈ (-∞; -2) U (-1; +∞)
3. 2x - 6 ≤ 0 ⇒ 2x ≤ 6 ⇒ x ≤ 3 ⇒ x ∈ (-∞; 3]
x²+7x+6 > 0 ⇒ x²+7x+6=0 ⇒ D = 49 - 24 = 25 ⇒ x₁₂ = -1; -6 ⇒ (x+1)(x+6)>0 ⇒ x ∈ (-∞;-6) U (-1; +∞)
Находим пересечения (как показано в 4 задании)
Ответ: x ∈ (-∞; -6) U (-1; 3]
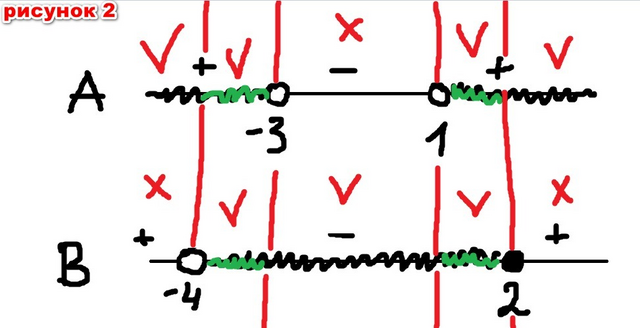
4. см рис 2. Ответ: x ∈ (-4; -3) U (1; 2]