ДАНО 
ИССЛЕДОВАНИЕ.
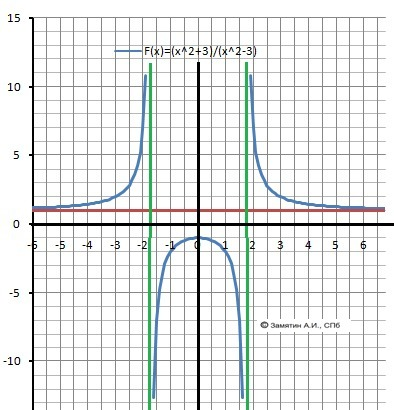
1.Область определения D(x).
x²- 3 = (x+√3)(x-√3) ≠ 0, x≠ +/- √3 ≈ +/- 1,73.
Два разрыва - две вертикальные асимптоты.
Х∈(-∞;-√3)∪(-√3;√3)∪(√3;+∞)
2. Вертикальные асимптоты - две: Х= -1,73 , Х= 1,73. На рисунке - зеленые.
3. Пересечение с осью Х. Y=0 - нет.
4. Пересечение с осью У. У(0) = -3/3 = -1.
5. Поведение на бесконечности. Сокращаем на х² - числитель и знаменатель.
limY(-∞) = (1+0)/(1-0) = 1. Справа Y=1. limY(+∞) = 1.
Горизонтальная асимптота - Y= 1 (на рисунке - красная).
6. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
7. Производная функции. - частное двух функций.

Корень при Х=0. График первой производной такой же форму, как и на втором рисунке в приложении.
8. Локальные экстремумы.
Максимум - Y(0) = -1 . Минимума - нет.
9. Интервалы монотонности.
Возрастает - Х∈[-∞;- √3)∪(-√3;0], убывает - X∈[0;√3)∪(√3;+∞)
10. Вторая производная - Y"(x). Анализируем первую производную. Максимума Y'(x) - нет - точек перегиба НА ГРАФИКЕ - нет.
11. Выпуклая “горка» Х∈(- √3;√3), Вогнутая–«ложка»Х∈(-∞;-√3)∪(√3;+∞).
12. Поведение в точках разрыва.
lim(-1-)Y(x) = +∞,lim(-1+)Y(x) = -∞,lim(1-)Y(x) =-∞,lim(1+)Y(x) = +∞,
13. График в приложении.