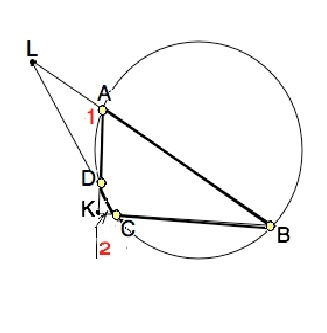
Сумма противолежащих углов вписанного четырехугольника равна 180°. Четырехугольник АВСD - вписанный, ⇒ ∠ВАD+∠BСD=180°. Угол ВАL - развернутый. Сумма смежных углов равна 180°. ⇒ ∠BАD +∠LAD =180°. На приложенном рисунке ∠ LAD обозначен как 1, а ∠KCD – 2. Следовательно, угол С =∠1.
Рассмотрим треугольники АLD и СКD. Вертикальные углы при D равны – Вычтя их из суммы углов треугольника, получим <1+<L=<2+<K</strong>. По условию ∠К=60°+ Заменим в предыдущем уравнении угол К найденным значением: ∠1+∠L=<2+60°+∠</strong>L, откуда ∠1=∠2+60°. Равный углу 1 ∠С=∠2+60° , ⇒ ∠2=∠С-60°, поэтому ∠С-60°+∠С=180°, ⇒ 2С=240°, ∠С=120° и, следовательно, угол ВАD=60°