Стереометрия помогите срочно, номер 19!!!

Question

Дан 1 ответ

Правильный ответ

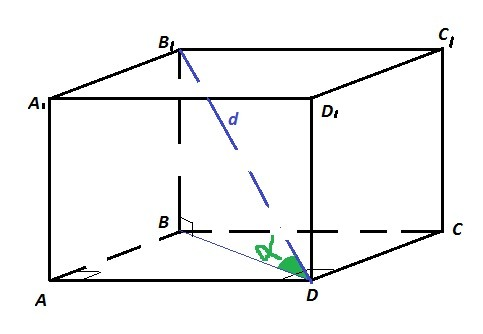
Дано: правильная четырёхугольная призма ABCDA₁B₁C₁D₁ ; AB=BC=CD=AD; B₁B⊥(ABC); B₁D=d - диагональ призмы; B₁DB=α - угол наклона диагонали к основанию призмы.

Найти : $S_{BB_1D_1D}$ ; Sбок ; Sосн

ΔBB₁D - прямоугольный, ∠B₁BD = 90°; B₁D = d; ∠B₁DB = α

Из соотношений в прямоугольном треугольнике :

BB₁ = d · sin α ; BD = d · cos α

В основании призмы лежит квадрат. Так как диагональ квадрата равна стороне квадрата, умноженной на √2, то

AB = AD = BD / √2 = d · cos α / √2

Площадь диагонального сечения-прямоугольника :

$\boldsymbol{S_{BB_1D_1D}=}BB_1\cdot BD = d\cdot sin~\alpha~\cdot d~\cdot cos~\alpha=\\ \\ =\dfrac{d^2\cdot 2 sin~\alpha~cos~\alpha}{2}=\boldsymbol{0,5d^2\cdot sin~(2\alpha)}$

Площадь боковой поверхности :

Sбок = 4·AB·BB₁ = $4\cdot \dfrac{d\cdot cos~\alpha }{\sqrt{2} }\cdot d\cdot sin~\alpha =\dfrac{2\cdot d^2\cdot (2\cdot cos~\alpha \cdot sin~\alpha)}{\sqrt{2} }$

Sбок = $\boldsymbol{\sqrt{2} \cdot d^2\cdot sin~(2\alpha)}$

Площадь основания :

Sосн = AB² = $\Big(\dfrac{d\cdot cos~\alpha}{\sqrt{2} }\Big)^2=\boldsymbol{0,5d^2\cdot cos^2\alpha }$

==============================================

Использована формула синуса двойного аргумента :

2 sin α cos α = sin (2α)

xERISx_zn (41.0k баллов) 17 Май, 20