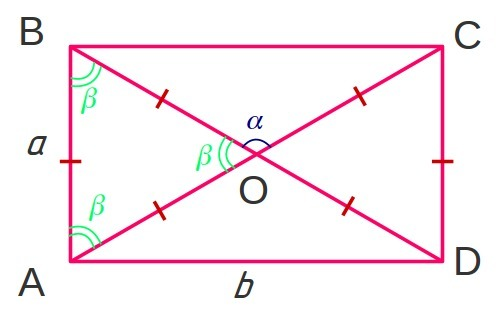
Смотрите поясняющий рисунок.
Если один из углов межу диагоналями α=120°, то другой β=30°.
Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит малые треугольники будут равнобедренными, углы при основании равны. Значит в остроугольных треугольниках ΔABO и ΔDOC углы при сторонах AB CD (=a) будут равны (180-30)/2=60°=β. Т.е. треугольники ΔABO и ΔDOC будут равносторонними и следовательно половины диагоналей AO=BO=CO=DO= a . Соответственно диагонали AC=BD=2a
Из прямоугольного ΔABD выражаем квадрат гипотенузы (диагонали прямоугольника) BD:
 [1]
[1]
Площадь прямоугольника
 [2]
[2]
Выражаем сторону b через a и площадь S.
 [3]
[3]
Подставляем [3] в [1] и решаем полученное уравнение.
![\frac{S^2}{a^2}+a^2=(2a)^2=4a^2\\ \\ S^2=4a^4-a^4=3a^4\\ \\ a=\sqrt[4]{\frac{S^2}{3} }=\sqrt[4]{\frac{81}{3}}=\sqrt[4]{27} =3^{\frac{3}{4} } \frac{S^2}{a^2}+a^2=(2a)^2=4a^2\\ \\ S^2=4a^4-a^4=3a^4\\ \\ a=\sqrt[4]{\frac{S^2}{3} }=\sqrt[4]{\frac{81}{3}}=\sqrt[4]{27} =3^{\frac{3}{4} }](https://tex.z-dn.net/?f=%5Cfrac%7BS%5E2%7D%7Ba%5E2%7D%2Ba%5E2%3D%282a%29%5E2%3D4a%5E2%5C%5C%20%5C%5C%20S%5E2%3D4a%5E4-a%5E4%3D3a%5E4%5C%5C%20%5C%5C%20a%3D%5Csqrt%5B4%5D%7B%5Cfrac%7BS%5E2%7D%7B3%7D%20%7D%3D%5Csqrt%5B4%5D%7B%5Cfrac%7B81%7D%7B3%7D%7D%3D%5Csqrt%5B4%5D%7B27%7D%20%20%3D3%5E%7B%5Cfrac%7B3%7D%7B4%7D%20%7D)
Соответственно из [3] находим b.
![b=\frac{S}{a} =\frac{9}{\sqrt[4]{27} } =3^{2} \cdot 3^{-\frac{3}{4} }=3^{\frac{8-3}{4} }=3^{\frac{5}{4} }=\sqrt[4]{3^5} =\sqrt[4]{243} b=\frac{S}{a} =\frac{9}{\sqrt[4]{27} } =3^{2} \cdot 3^{-\frac{3}{4} }=3^{\frac{8-3}{4} }=3^{\frac{5}{4} }=\sqrt[4]{3^5} =\sqrt[4]{243}](https://tex.z-dn.net/?f=b%3D%5Cfrac%7BS%7D%7Ba%7D%20%3D%5Cfrac%7B9%7D%7B%5Csqrt%5B4%5D%7B27%7D%20%7D%20%3D3%5E%7B2%7D%20%5Ccdot%203%5E%7B-%5Cfrac%7B3%7D%7B4%7D%20%7D%3D3%5E%7B%5Cfrac%7B8-3%7D%7B4%7D%20%7D%3D3%5E%7B%5Cfrac%7B5%7D%7B4%7D%20%7D%3D%5Csqrt%5B4%5D%7B3%5E5%7D%20%3D%5Csqrt%5B4%5D%7B243%7D)
Ответ:
![a=\sqrt[4]{27} \\ \\ b=\sqrt[4]{243} a=\sqrt[4]{27} \\ \\ b=\sqrt[4]{243}](https://tex.z-dn.net/?f=a%3D%5Csqrt%5B4%5D%7B27%7D%20%5C%5C%20%5C%5C%20b%3D%5Csqrt%5B4%5D%7B243%7D)