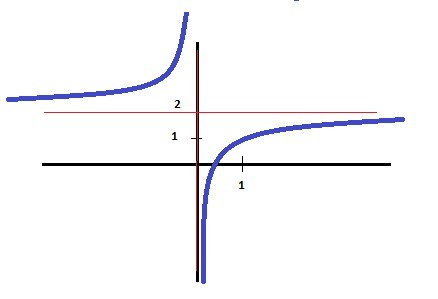
ДАНО: y = 2 - (x+4)/(x²+4*x)
ПОСТРОЕНИЕ
1. Область определения. x²+4*x = x*(x+4) ≠ 0. x≠0.
X∈(-∞;0)∪(0;+∞).
Точка разрыва - вертикальная асимптота: х = 0. (начертили)
2. Пересечение с осью У - нет - функция не существует.
3. Пересечение с осью Х.
2 - (х+4)/(х*(х+4)) = 2- 1/х = 0. х= 1/2 - ставим точку на оси.
4. Горизонтальная асимптота по формуле:

Проводим горизонтальную асимптоту.
5. Поведение в точке разрыва - при х= 0.
y(0-) = +∞ - слева от 0., y(0+) = - ∞ - справа от 0
Проводим графи к получаем рисунок в приложении.
Такой же график можно получить смещением графика Y=-1/X вверх на +2.