Боковое ребро правильной треугольной пирамиды равно 10, а сторона основания равна ....

Question 1

Боковое ребро правильной треугольной пирамиды равно 10, а сторона основания равна . Найдите высоту пирамиды.

Question 2

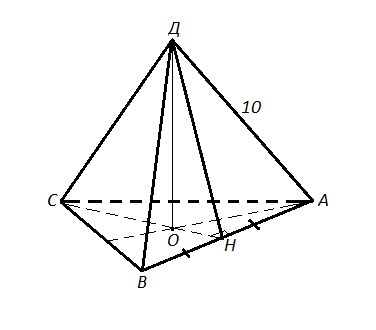
АВСД - прав. треуг. пирамида , АД=10 , АВ=АВ=ВС=а=6√3 , ДО⊥ пл. АВС , точка О - центр ΔАВС, то есть это точка пересечения медиан (высот, биссектрис) ΔАВС. Найти ДО.

Проведём СН⊥АВ , СО=2/3*СН=2/3*(а√3/2)=2/3*(6√3*√3/2)=6 .

ΔАОД: АО=СО=6 , АД=10 ⇒ ДО=√(АД²АО²)=√(100-36)=√64=8

Question 3

2:1 --> Всего на 2+1=3 части разбита медиана, из них 2 части приходится на СО и 1 часть на ОН.

Question 4

Это одна из основных теорем в геометрии ( причём это свойство верно для любого треугольника (не только правильного)

Question 5

Спасибо!

Question 6

Почему CH= a корень из 3/2?

Question 7

это уже формула нахождения в правильном треугольнике его высоты (все три высоты равны между собой), которая явл. и медианой и биссектрисой. По теореме Пифагора из треуг.СВН: корень(a^2-(a/2)^2)=корень(3a^2/4)=а*(корень из 3)/2. Впечатление, что вы в школу в 7-9 классах не ходили.

Question 8

такие вещи уже на автоматизме должны быть известны

Question 9

Так-то с геометрией оно и есть) в 9 кл готовилась по огэ задачам только, в 10 начала уже нормально заниматься. Спасибо

Question 10

По идее, в школе требуют, чтобы для правильного треугольника наизусть помнили формулу площади, длины высоты (медианы и биссектрисы), радиусов вписан. и описан. окружностей через длину стороны а, чтобы каждый раз не выводить заново эти вещи.

Question 11

Кстати, радиус описанной окр. - это СО=2/3*СН, а радиус вписанной окр. - это ОН=1/3*СН.

Question 12

Спасибо :*