Условие задачи записано неточно.
Правильно:
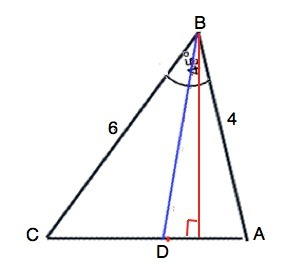
В треугольнике АВС АВ=4, ВС=6, ВD - биссектриса; угол АВС = 45°. Найдите площади треугольников АВD и СВD
a)
Одна из формул площади треугольника
S=0,5•a•b•sin α, где а и b - стороны, α – угол между ними.
S (АВС)=0,5•4•6•√2/2=6√2
б)
В треугольниках ABD и CBD высоты из В к основаниям совпадают. Площади треугольников с равными высотами относятся как их основания.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам (свойство) ⇒
АD:DC=AB:CB=2:3 ⇒
S(∆ ABD):S(∆BCD)=АD:DC=AB:CB=2:3
S(∆ ABD)+S(∆BCD)=5 частей= 6√2
S(∆ ABD)=(1/5•6√2)•2=2,4√2(ед.площади)
S(∆BCD)=(1/5•6√2)•3=3,6√2 (ед. площади).