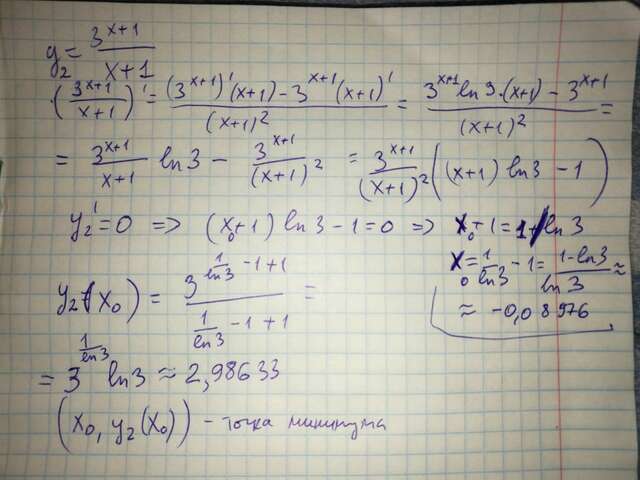Это не уравнение у Вас, а неравенство
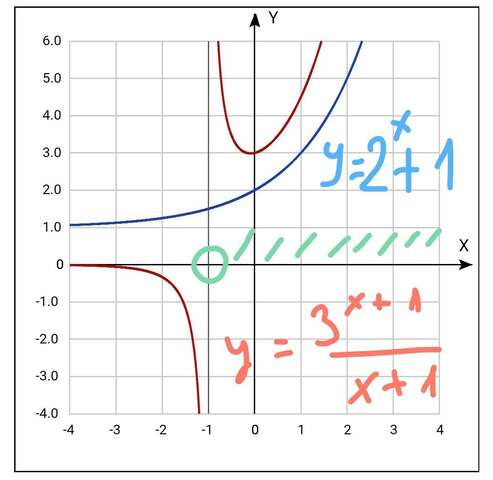
1^x +2^x< 3^(x+1)/(x+1)
1 +2^x< (3^(x+1))/(x+1)
построим графики
у1(х) = 1 + 2^x
у2(х) = (3^(x+1))/(x+1)
первый график y1(x) получается сдвигом графика 2^х на единицу вверх вдоль оси ординат
Вторая функция у2(х) является произведением двух функций
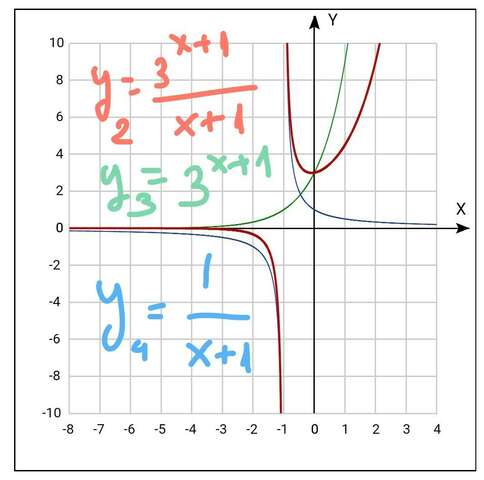
у2(х)=у3(х)•у4(х), где
у3(х)=3^(х+1) -
степенная функция,
строится переносом графика 3^х на 1 влево вдоль оси абсцисс
у4(х)=1/(х+1) -
гипербола, которая получается из гиперболы 1/х переносом её на 1 влево вдоль оси абсцисс.
Поэтому для построения
у2(х) поступаем так.
Берем точку (х*) , её ордината
у2(х*) находится как произведение ординат
у3(х*)•у4(х*)
у2(х*)=у3(х*)•у4(х*)
Свойства у2(х):
функция определена на
Dy2(x):х€(-∞, -1)v(-1,+∞)
область значений у2(х)
Ey2(x):y€(-∞,0)v(0,+∞)
ассимптоты для у2(х)
х=-1 и у=0
функция не является четной или нечетной, т.к.
у2(-х)=(3^(-x+1))/(-x+1))≠
≠у2(х)
у2(-х)≠-у2(х)
функция не является периодичной, т.к.
не существует T, такого что y2(x+T)=y2(x)
у2(х) не имеет нулей ,она не пересекает ОХ.
у2(х) пересекает
ось ОУ в точке
(0;у2(0))=(0;3)
у2(х)>0 при х>-1
у2(х)<0 при х<-1<br> найдем производную у2(х)
(см приложение)
функция убывает, когда у2'(х)<0<br>при
х€(-∞;-1)v(-1; ((1-ln3)/ln3) )
функция возрастает
при у2'(х)>0
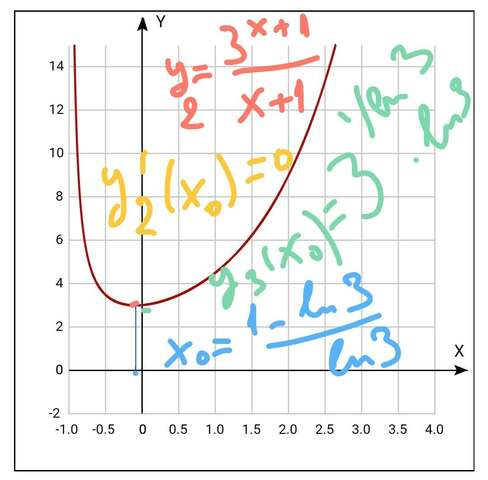
у2'(х°)=0=> х°=((1-ln3)/ln3)
(х°;у2(х°))- точка минимума у2(х)
(см рисунок)
график приведен на рисунке
Решением нашего неравенства
будет область, где у1 (х) будет находится под графиком у2(х) при одинаковых значениях х.
Нетрудно видеть,
что это будет при х> - 1
Ответ х> - 1