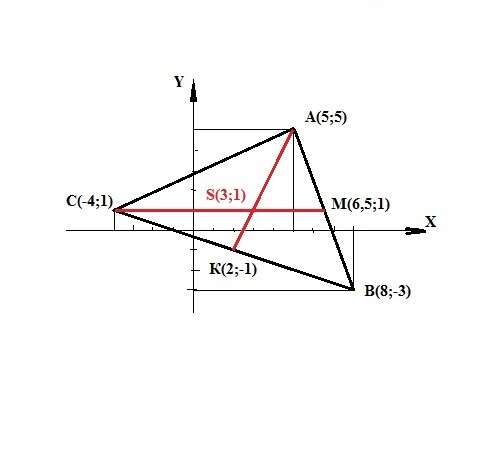
Найдем координаты точек М (середина отрезка АВ) и К (середина отрезка ВС) :
Хм=(Хa+Xв):2 =(5+8):2 = 6,5; Yм=(Ya+Yв):2 =(5-3):2 = 1. => M(6,5;1).
Хк=(Хв+Xс):2 =(8-4):2 = 2; Yк=(Yв+Yс):2 =(-3+1):2 = -1. => К(2;-1).
Уравнение прямой СМ: (X-Xc)/(Xm-Xc)=(Y-Yc)/(Ym-Yc) или
(X+4)/(6,5+4)=(Y-1)/(1-1) => Y=1 (1).
Уравнение прямой АК: (X-Xа)/(Xк-Xа)=(Y-Yа)/(Yк-Yа) или
(X-5)/(2-5)=(Y-5)/(-1-5) => 2X-Y=5 (2).
Решая систему уравнений (1) и (2), получаем координаты точки пересечения медиан: S(3;1) Это ответ.
А можно так: Середина К отрезка ВС:К(2;-1). (Найдена выше). Отрезок АК (медиана) точкой пересечения делится в отношении 2:1, считая от вершины А (свойство). Если известны две точки плоскости А(Xa;Ya) и К(Xk;Yk) , то координаты точки S(Xs;Ys), которая делит отрезок АK в отношении λ=АО/ОК=2/1, выражаются формулами: Хs=(Xa+λ*Xk)/(1+λ) и Ys=(Ya+λ*Yk)/(1+λ).
В нашем случае:
Xs=(5+2*2)/3 = 3.
Ys=(5+2*(-1))/3 = 1.
Ответ: S(3;1)