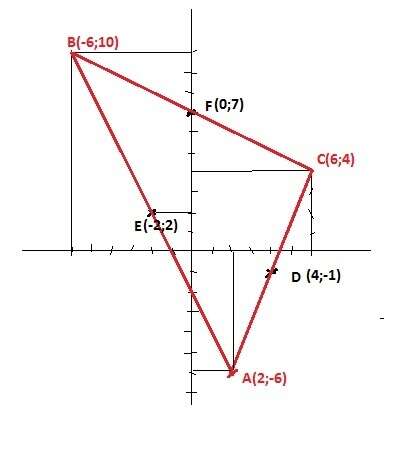
Пусть точка Е(-2;2) - середина стороны АВ, Точка F(0;7) - середина стороны ВС и точка D(4;-1) - середина стороны АС.
Координаты середины отрезка AB находятся по формулам: X= (Хa+Xb)/2; Y= (Ya+Yb)/2. Тогда
Xe = (Xa+Xb)/2 = -2; => Xa+Xb=-4. Ye = (Ya+Yb)/2 = 2; => Ya+Yb = 4.
Xf = (Xc+Xb)/2 = -2; => Xc+Xb=0. Yf = (Yc+Yb)/2 = 7; => Yc+Yb =14.
Xd = (Xa+Xc)/2 = -2; => Xa+Xc=8. Yd = (Ya+Yc)/2 = -2; => Ya+Yc = -4.
Имеем системы уравнений: Xa+Xb= -4.
Xc+Xb=0.
Xa+Xc=8. => Xa = 2; Xc = 6; Xb = -6.
Ya+Yb = 4.
Yc+Yb =14.
Ya+Yc = -2. => Ya = -6; Yc = 4; Yb = 10.
Ответ: А(2;-6), В(-6;10), С(6;4).
P.S. Рисунок для проверки.