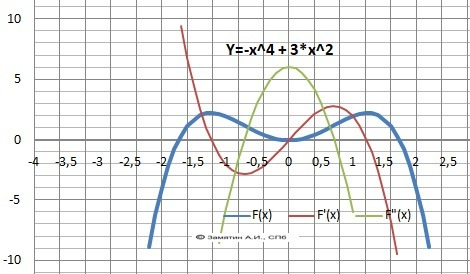
ДАНО: F(x) = 3*x² - x⁴
НАЙТИ: Экстремумы функции.
РЕШЕНИЕ: Экстремумы находятся в корнях первой производной.
F'(x) = 6*x - 4*x³ = - x*(4*x² - 6) = - х*(x² - 3/2) = 0.
Корни: х1 = 0, x2 = - √(3/2) ≈ - 1,22, х3 = √(3/2) ≈ 1,22.
Вычисляем экстремумы: Сначала х₂² = 1,5, х₂⁴ = 2,25.
Минимум - У(0)= 0.
Функция чётная. Максимумы - У(х₂) = У(х₃) = 3*1,5 - 2,25 = 2,25.
Рисунок с графиками исследования функции на рисунке в приложении.
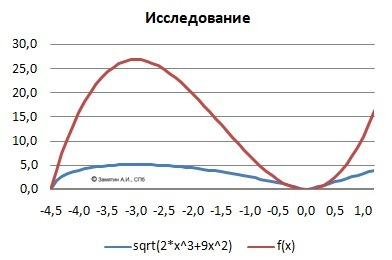
ДАНО: F(x) =√(2х³ + 9х²)
F(x) = x*√(2x+9) - преобразовали.
ОДЗ 2х+9>0 и х> -4.5 или X∈[-4.5;+∞).
Радикал - возрастающая функции и, поэтому, производную возьмём от подкоренной функции.
f(x) = 2*x³ + 9*x² и f'(x) =6*x² + 18*x = 6*x*(x+3).
Корни: х1 = 0, х2 = -3 - точки экстремумов.
Значения экстремумов:
Максимум: F(-3) = √(2*(-27) + 9*9) = √27 = 3*√3 ≈ 5.196
Минимум: F(0) = 0.
Рисунок к задаче в приложении.