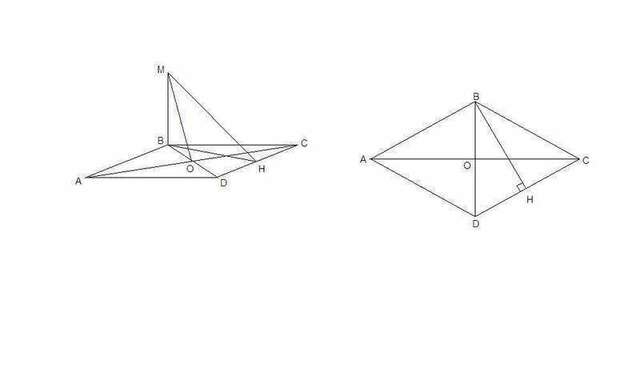
Если в ромбе угол равен 60°, то его меньшая диагональ равна стороне (АВ = AD как стороны ромба, ΔАBD равнобедренный с углом 60°, значит и остальные углы по 60°, т.е. ΔАВD равносторонний).
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к прямой.
Пусть Н - середина CD, тогда BH - медиана и высота в равностороннем треугольнике BCD.
ВН⊥CD.
ВН - проекция МН на плоскость АВС, значит
МН⊥CD по теореме о трех перпендикулярах.
МН = 6 см - расстояние от точки М до прямой CD.
ВН = ВС√3/2 = 6√3/2 = 3√3 см как высота равностороннего треугольника
Из ΔМВН по теореме Пифагора:
МВ = √(МН² - ВН²) = √(36 - 27) = √9 = 3 см
ВО⊥АС так как диагонали ромба перпендикулярны.
ВО - проекция МО на плоскость АВС, значит
МО⊥АС по теореме о трех перпендикулярах.
МО - искомое расстояние от точки М до прямой АС.
ВО = BD/2 = 6/2 = 3 см
Из ΔМВО по теореме Пифагора:
МО = √(МВ² + ВО²) = √(9 + 9) = √18 = 3√2 см