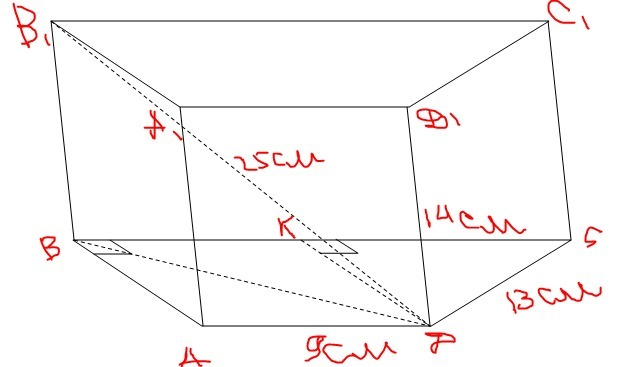
Площу бічної поверхні знайдемо за формулою S = P₀·h, де P₀ = АВ + АД + ДС + ВС; h = ВВ₁
Проведемо висоту трапеції КД, тоді ΔКДС - прямокутний (∠КДС = 90°).
З ΔКДС: КД = √(ДС² - КС²), де КС = ВС - ВК = 14 - 9 = 5 см (ВК = АД = 9 см, як протилежні сторони прямокутника ВКДС). Звідси, КД = √(13² - 5²) = 12 см.
З ΔВКД (∠ВКД = 90°): ВД = √(ДК² + КВ²) = √(12² + 9²) = 15 см
З ΔВВ₁Д (∠ВВ₁Д = 90°): ВВ₁ = √(ДВ₁² - ДВ²) = √(25² - 15²) = 20 см
Отже, P₀ = 12 + 9 + 13 + 14 = 48 см; S = 48·20 = 960 см².