** одной кондитерской фабрике провели исследование причин образования затора из конфет **...

Question

На одной кондитерской фабрике провели исследование причин
образования затора из конфет на ленте транспортера перед упаковочной машиной.
Оказалось, что в зависимости от концентрации конфет (их числа на 1 м длины
ленты транспортера) упаковочная машина автоматически корректирует скорость
ленты, чтобы справиться с упаковкой. Исследователи свои результаты представили
на графике зависимости скорости ленты от концентрации конфет на ней. Из графика
видно, что при больших скоростях ленты упаковочная машина, из-за особенностей
механизма срабатывания, успевает обрабатывать небольшие концентрации конфет.
При больших концентрациях приходится скорость ленты сильно снижать и
производительность конвейера падает. Какое максимальное количество конфет в
минуту может обработать упаковочная машина? Масштаб по осям графика дан в
условных единицах кратных 0,1 м/с и 1 конфет/метр. Округлить до целых.

---

Answer 1

Пусть при концентрации n скорость транспортёра v, и угловой коэффициент наклона зависимости v(n)=-a<=0. Попробуем немного увеличить концентрацию конфет на dn. Тогда прирост производительности будет равен:<br>(v - a*dn)(n + dn) - v*n = (-a*n + v) dn - a*dn^2
dn^2 - мало и им можно пренебречь. Останется член (-a*n + v)*dn. Если выражение в скобках будет положительным, то выгодно увеличивать концентрацию, если отрицательным - уменьшать.
Итак, если v>a*n, выгодно увеличивать концентрацию, если меньше - уменьшать.
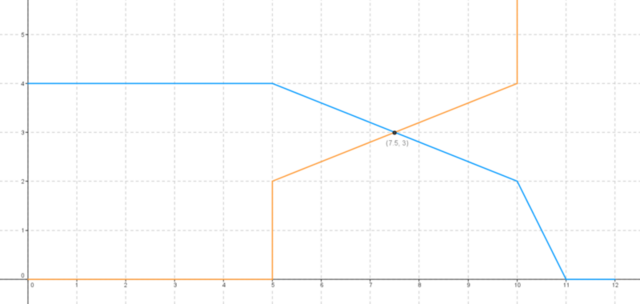
Неравенство v > a*n можно, например, решать графически. Из графика (см. вложение) находим, что максимальное количество конфет машина обработает, если n = 7,5 ~ 7.5 конфет/метр и v = 3 ~ 0.3 м/с. Искомая производительность равна 7,5*0,3 примерно 2 конфеты/сек

---

Comments

я не согласен с решением ведь сказано что масштаб дан не конкретным числом а числом кратным ему