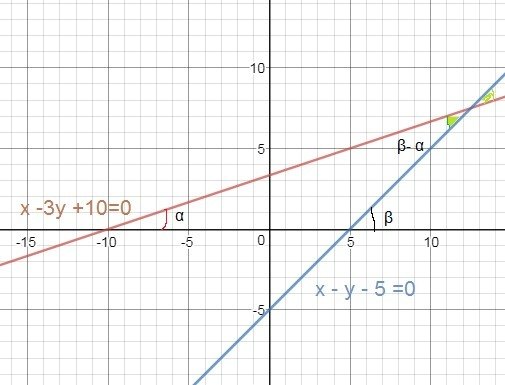
x-3y+10=0 ⇒ y=(1/3)x+(10/3)⇒ k₁=1/3 ⇒ tgα=1/3
α - угол, который образует прямая x-3y+10=0 с положительным направлением оси Ох;
x-y-5=0 ⇒ y=x-5 ⇒ k₂=1⇒ tgβ=1
β - угол, который образует прямая x-y-10=0 с положительным направлением оси Ох;
Тогда угол между прямыми равен (β-α)
tg(β-α)=(tgβ-tgα)/(1+tgβ·tgα)=(1-(1/3))/(1+(1/3))=(2/3)/(4/3)=1/2
О т в е т. β-α= arctg(1/2)