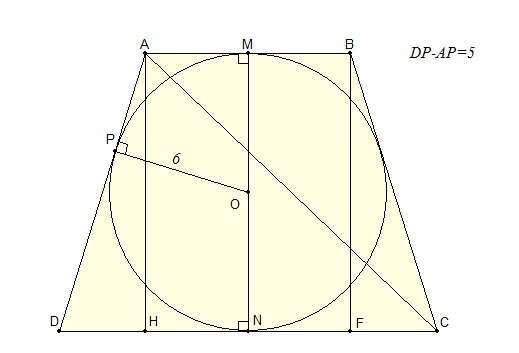
Смотрите рисунок во вложении
Поскольку в трапецию можно вписать окружность, то выполняется условие AB+CD=BC+AD или AB+CD=2BC (трапеция равнобедренная). По-этому, если обозначить AP=x и учесть свойство касательной к окружности, имеет место уравнение

Высота трапеции будет равна диаметру 2r данной окружности:

Поскольку AM=MB=FN=HN, то DH=FC=10:2=5 и по теореме Пифагора

Тогда из уравнения

получим, что AB=2x=8, a CD=AB+2DH=8+10=18 и средняя линия трапеции будет равна (AB+CD):2=13.