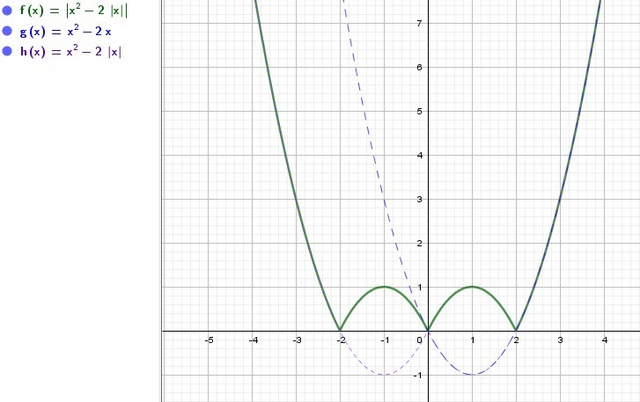
1. Строим сначала график функции y = x² - 2x. Графиком квадратичной функции является парабола, ветви которого направлены вверх.
(1;-1) - координаты вершины параболы.
2.График функции y = x² - 2x симметрично отобразим относительно оси ординат, получим график функции y = x² - 2|x|
3. Нижнюю часть графика функции y = x² - 2|x| симметрично отобразим относительно оси Ох в положительную часть оси ординат, в результате получим график функции y = |x² - 2|x||
Графиком функции y = a-1 является прямая, параллельная оси Ох.
1) При a-1=0 откуда а=1 графики функций имеют три общих точек, следовательно, уравнение имеет три решения.
2) При 0 < a-1 < 1 откуда 1 < a < 2 графики пересекаются в 6 точках, следовательно уравнение имеет 6 решений.
3) При а - 1 = 1 откуда а=2 графики имеют четыре общих точек, следовательно, уравнение имеет ровно 4 решений
4) При a-1 > 1 откуда a>2 графики имеют две общих точек, значит уравнение имеет два решения