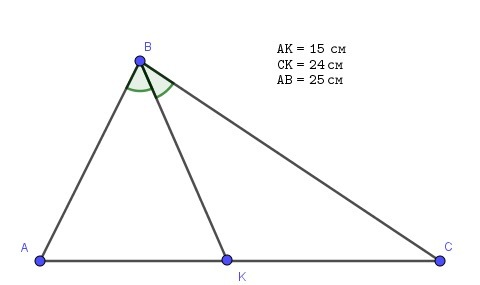
Биссектриса угла делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:

Имеем известные стороны: AB = 25 см, BC = 40 см и AC = AK+KC=15+24=39 см. Поскольку известны все стороны, то площадь треугольника будем искать по формуле Герона:
 см - полупериметр.
см - полупериметр.

Ответ: 468 см².