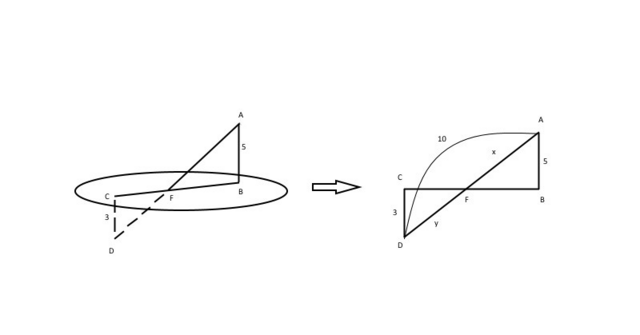
AD=10, AB=5, CD=3, BC - ?
Задача полностью решается через планиметрию, поэтому можно упростить чертеж.
Треугольники ABC и CFD прямоугольные, что очевидно из условия задачи. ∠AFB=∠CFD как вертикальные, отсюда sin∠AFB=sin∠CFD.
Обозначим AF=x, FD=y. Можно составить систему уравнений, используя ранее полученное равенство синусов.

Теперь теорема Пифагора

Ну и завершающий штрих

Ответ: 6