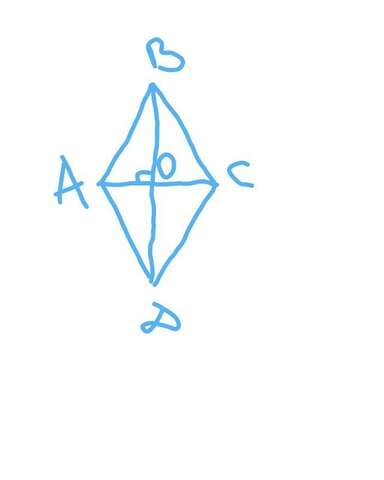1) Диагонали ромба точкой пересечения делятся пополам =>
AO = 1/2 * AC = 1/2 * 6 = 3 (см),
BO = 1/2 * BD = 1/2 * 6*sqrt(3) = 3*sqrt(3) (см)
2) Рассмотрим треугольник AOB: угол AOB = 90° (т.к. диагонали ромба пересекаются под прямым углом), AO = 3 см, BO = 3*sqrt(3) см.
tgABO = AO/BO = 3/3sqrt(3) = 1/sqrt(3) = sqrt(3)/3 => угол ABO = 30°.
3) Т.к. диагонали ромба являются биссектрисами, то угол ABC = 2*угол ABO = 2*30° = 60°
Ответ: 60°