Прямые ОВ и СD параллельные, а ОА и СD – скрещивающиеся прямые. Найдите угол между...

Question

Прямые ОВ и СD параллельные, а ОА и СD – скрещивающиеся прямые.
Найдите угол между прямыми ОА и СD, если угол АОВ = 135°.
Варианты ответа

1 0°
2 45°
3 135°

Comments

Смотря какой угол если внутренний то 180-135=45 если внешний то 135 это из-за того что углы AOB и CXO на крест лежащие (X - точка пересечения OA и CD

---

так какой ответ?

---

Матов, Вы ошибаетесь. Необходим острый угол ( 0°< a < 90° )

Answer 1

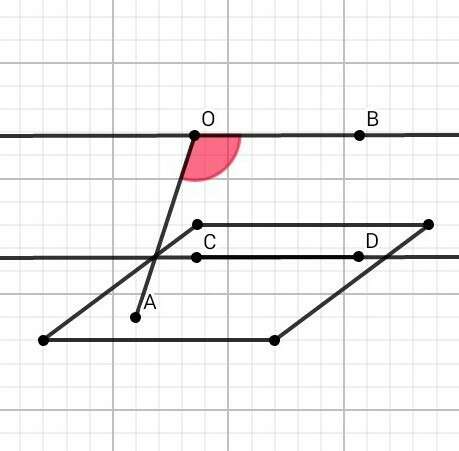
Чтобы найти угол между скрещивающимися прямыми, необходимо осуществить параллельный перенос одного из скрещивающихся прямых на другую прямую
Так как по условию ОВ || CD
Значит, угол между скрещивающимися прямыми ОА и CD равен углу между прямыми ОА и ОВ
Но по условию угол АОВ = 135°
Из этого следует, что и угол между скрещивающимися прямыми ОА и CD равен 135°
Но углом между скрещивающимися прямыми называется угол наименьшей градусной меры →
180° – 135° = 45°

ОТВЕТ: 2) 45°

---

Comments

идеальному ответу большое спасибо)