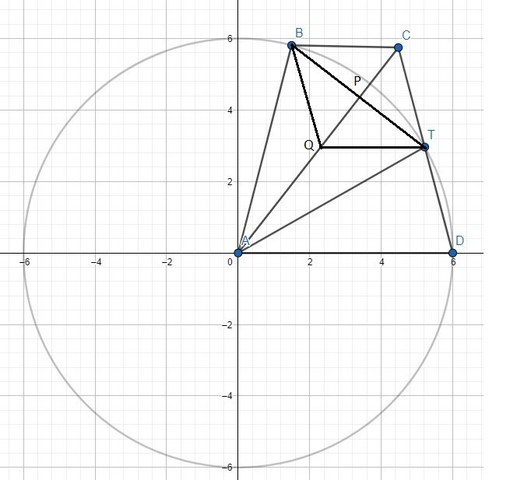
Проведём в треугольнике ACD среднюю линию. Она пересечёт AC в точке Q (запомним, что QC принадлежит AC). При этом QT || AD, и следовательно QT || BC. Видим, что QT=AD/2. Сторона BС также равна AD/2, следовательно BС=QT. Т.к. BС=QT и BС || QT, то BCTQ-параллелограмм. Получается, что точка Q является как вершиной параллелограмма, как и точкой на отрезке AC.
Проведём к хорде BT медиану AP. При этом треугольники ABP и ATP будут равны по 3-м сторонам, т.к. AB=AT, BP=PT, AP - общая. Следовательно, углы APB и APT в этих треугольниках равны, а т.к. эти углы смежные, то они равны 90 градусов. Получается, что AP является перпендикуляром к хорде.
QC и BT - диагонали параллелограмма, которые пересекаются в их серединах, но т.к. AP - медиана => P - середина BT, то точка P принадлежит также QC, а т.к. QC принадлежит AC (см. ранее), то и P принадлежит AC, т.е. точки Q и P лежат на AC.
Точки A и P лежат, как на AP, так и на AC, следовательно AP и AC лежат на одной прямой.
Т.к. AP перпендикулярен BT, то и QC перпендикулярен BT. Диагонали QC и BT параллелограмма QBCT перпендикулярны, следовательно QBCT является ромбом => BQ=BC=CT=QT.
Треугольники BAQ и TAQ равны по трём сторонам. У них AB=AT, BQ=QT, AQ-общая => равны углы BAQ и TAQ => равны углы BAC и TAC