Найдём область определения функции и упростим выражение.
 3} \atop {\frac{(x-3)^2}{-(x-3)}=3-x\; ,\; esli\; \; x<3}} \right. " alt=" y=\frac{x^2-6x+9}{|x-3|}\; \; ,\; \; ODZ:\; |x-3|\ne 0\; ,\; x-3\ne 0\; ,\; x\ne 3\\\\\frac{x^2-6x+9}{|x-3|}=\frac{(x-3)^2}{|x-3|}=\left \{ {{\frac{(x-3)^2}{x-3}=x-3\; ,\; esli\; \; x>3} \atop {\frac{(x-3)^2}{-(x-3)}=3-x\; ,\; esli\; \; x<3}} \right. " align="absmiddle" class="latex-formula">
3} \atop {\frac{(x-3)^2}{-(x-3)}=3-x\; ,\; esli\; \; x<3}} \right. " alt=" y=\frac{x^2-6x+9}{|x-3|}\; \; ,\; \; ODZ:\; |x-3|\ne 0\; ,\; x-3\ne 0\; ,\; x\ne 3\\\\\frac{x^2-6x+9}{|x-3|}=\frac{(x-3)^2}{|x-3|}=\left \{ {{\frac{(x-3)^2}{x-3}=x-3\; ,\; esli\; \; x>3} \atop {\frac{(x-3)^2}{-(x-3)}=3-x\; ,\; esli\; \; x<3}} \right. " align="absmiddle" class="latex-formula">
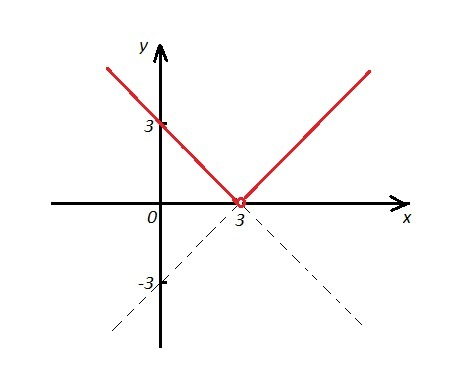
Cтроим прямую у=х-3 при x>3 и у=3-х при х<3, причём при х=3 функция не определена. Поэтому из графика выколем точку (3,0).</p>
P.S. Можно заметить, что  и упростить функцию таким образом:
и упростить функцию таким образом:  .
.
И тогда построить график функции у=|x-3|. Для этого строят график у=х-3, а затем отображают часть прямой, лежащую ниже оси ОХ, в верхнюю полуплоскость. И , учитывая ОДЗ, выкалываем точку (3,0). (Получим тот же график.)