25 БАЛЛОВ Дано : Квадрат ABDC . Сторона квадрата 10 см. AF=FB FK=KD LK перпендикулярно...

Question

25 БАЛЛОВ
Дано : Квадрат ABDC . Сторона квадрата 10 см.
AF=FB
FK=KD
LK перпендикулярно FD
LK - ?

---

Comments

Рисунок неверный. К -середина FD. Если LK перпендикулярна FD, то прямой угол составляет не с АD, а с DK/

Answer 1

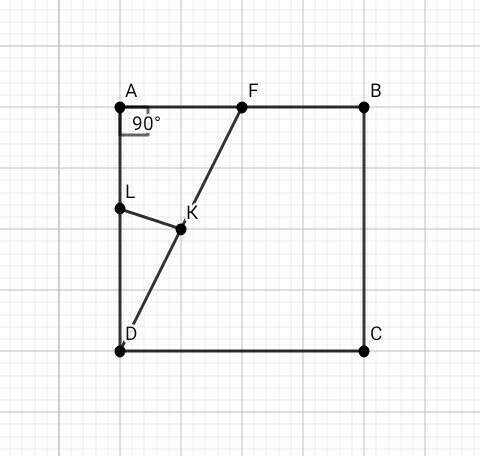
ДАНО: АВСD – квадрат, АВ = 10 см , AF = FB , FK = KD , LK перпендикулярен FD

НАЙТИ: LK
____________________________

РЕШЕНИЕ:

AF = FB = ( 1/2 ) × AB = ( 1/2 ) × 10 = 5 см

Рассмотрим ∆ DAF (угол DAF = 90°):
По теореме Пифагора:
DF² = AD² + AF²
DF² = 10² + 5² = 100 + 25 = 125
DF = 5√5 см
DK = KF = ( 1/2 ) × DF = ( 1/2 ) × 5√5 = 5√5 / 2 см

∆ DAF подобен ∆ DKL по двум углам ( угол DAF = угол DKL = 90° , угол D – общий )
Составим отношения сходственных сторон:
DK/ AD = LK/ AF = LD/ DF
( 5√5/2 ) / 10 = LK/ 5 →

LK = 5√5 / 4 см



ОТВЕТ: LK = 5√5 / 4 см

---

Comments

LK = 5√5 / 4=1,25√5 см

---

А я люблю писать ответ в виде дроби :)

---

Если учитель не возражает против такой записи, почему бы и нет?

---

Обычно учителя пишут ответ в виде дроби. И к тому же в задачниках ответы в виде дроби...

---

А если бы ответ был такой: 7√5 / 512 – Вы бы записали ответ таким образом – 0,013671875√5 ?

---

Шутить изволите? Но если в условии предлагается дать ответ "с точностью до.." (сотых, десятых и т.д) – записала бы.

---

Никто здесь и не шутит.

Answer 2

Судя по чертежу в условии опечатка, LK перпендикулярно AD

Ответ:
LK=2,5 см

решение приведено на фото

Удачи!

---

Comments

LK перпендикулярна FD. Решение должно учитывать условие, а не рисунок, сделанный автором вопроса,– он не соответствует условию.

---

Не соглашусь. Нельзя сказать однозначно. А может , в условии ошибка, раз так построено. Не собираюсь играть в угадайку и посему решил так. Пусть автор определится. А мы решим

---

Смысл примерно один, треугольники подобны. Только пропорция понятно получается разная.

---

Верно, только по рисунку слишком простое получается решение.