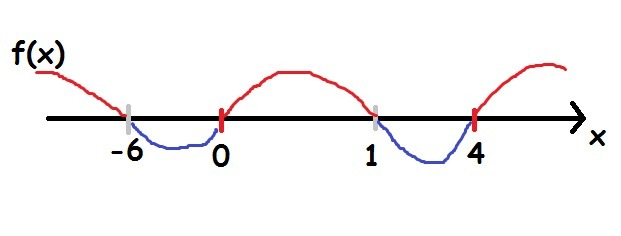
Насколько я понял, функция:

Во-первых, x² + 5x - 6 ≠ 0, потому что деление на ноль не определено. У x² + 5x - 6 = 0 два корня: 1 и -6.
Во-вторых,  , потому что (в данном контексте) корень из отрицательного числа не определён. Решим неравенство методом интервалов.
, потому что (в данном контексте) корень из отрицательного числа не определён. Решим неравенство методом интервалов.

Далее — см. вложение.
Нам нужны области, где выражение больше или равно нулю. Также нужно не забыть исключить точки, где выражение не определено, то есть 1 и -6.
Значит, ответ: