Область интегрирования ограничена линиями: x=0; x=1; y=-2x; y=√(4-x²)
Определим, что является графиком последней функции:

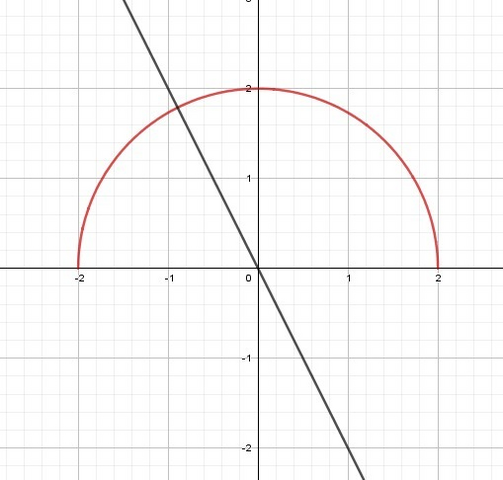
Графиком является верхняя полуокружность с радиусом R=2
1) строим графики y=-2x; y=√(4-x²) (рис.1)
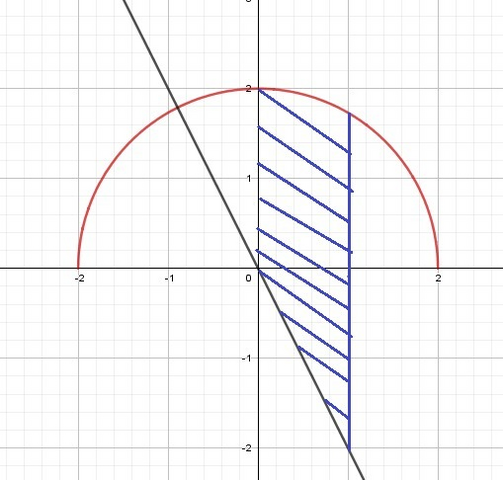
2) с учетом x=0 и x=1 получаем область интегрирования (заштрихованная область) (рис.2)
3) выражаем иксы через игреки и разбиваем исходный интеграл на 3 части (пользуясь рисунком 3)
ищем границы по игреку
зеленая область: от -2 до 0
синяя: от 0 до √3 (так как при х=1 получаем у=√(4-х²)=√(4-1)=√3)
красная: от √3 до 2


С полученными данными составляем окончательный ответ: