Решения не существует.
Минимальным периметром из всех треугольников при одном и том же радиусе вписанной окружности обладает равносторонний треугольник. Найдём его периметр.
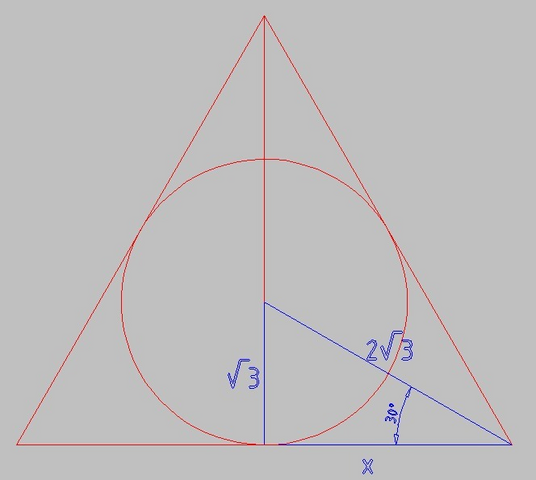
В синем треугольнике
короткий катет равен радиусу вписанной окружности исходного Δ, √3
гипотенуза в 2 раза длиннее короткого катета, и равна 2√3
Длинный катет по т. Пифагора
x² = (2√3)² - (√3)² = 4*3 - 3 = 9
x = 3
Сторона равностороннего треугольника
2x = 2*3 = 6
Периметр равностороннего треугольника
3*6 = 18
При том, что в условии задания указано, что периметр равен 9, ровно в 2 раза меньше минимально возможного.