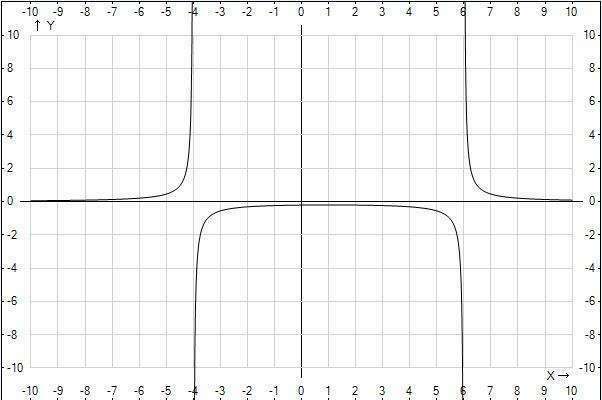
1) f ' (x) = (0 - 5*2*(x - 1)) / ((x - 1)^2 - 25)^2 = - 10(x - 1) / ((x - 1)^2 - 25)^2
f ' (x) = 0, x = 1
(x - 1)^2 - 25 ≠ 0, (x - 1)^2 ≠ 25, (x - 1) ≠ 5 и (x - 1) ≠ -5; x ≠ - 4, x ≠ 6
При x < -4, f'(x) > 0 - функция возрастает
При x < 1, f'(x) > 0 - функция возрастает
При x > 1, f'(x) < 0 - функция убывает
При x > 6, f'(x) < 0 - функция убывает
x = -4, x = 6 - асимптоты
Функция не является монотонной, т.к. есть точки, в которых функция не существует. График состоит из 4 частей. Для каждого интервала находим несколько точек, подставляя в исходное уравнение выбранные значения х.
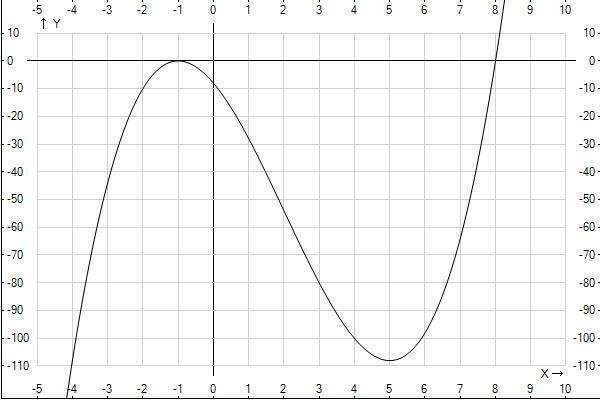
2) f'(x) = 3x^2 - 12x - 15 = 0
D = 144 + 4*15*3 = 324
x1 = (12 - 18) / 6 = -6/6 = -1
x2 = (12 + 18) / 6 = 30/6 = 5
При x < x1, f'(x) > 0 - функция возрастает
При x1 < x < x2, f'(x) < 0 - функция убывает
При x > x2, f'(x) > 0 - функция возрастает
x1 - точка максимума
x2 - точка минимума
f(-1) = -1 - 6 + 15 - 8 = 0
f(5) = 125 - 150 - 75 - 8 = -108
Пересечение с осью Ох: f(x) = 0, x = 8