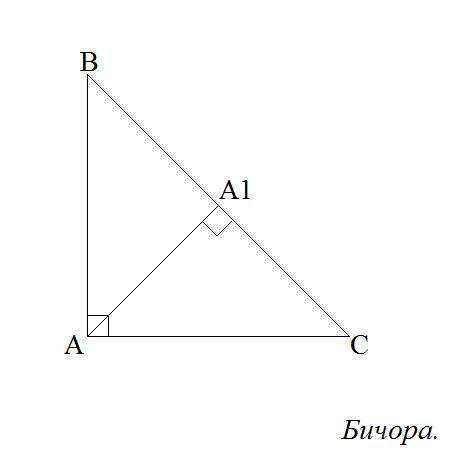
Чертеж во вложении.
1) Проведем высоту АА1= 7см.
2) По условию тр-к АВС- равнобедренный (АВ=АС) и прямоугольный (угол А=90), значит угол В= углу С= 45.
3) Рассмотрим тр-к АА1С: угол АА1С =90 и угол С=45, значит этот тр-к равнобедренный. АА1=А1С=7 см.
4) Тр-к АА1С= тр-ку АА1В (по гипотенузе и острому углу: АВ=АС и угол В= углу С). Значит, ВА1=А1С=7 см. Тогда ВС=14 см.
5)

см^2.
6) площадь прямоуг. тр-ка равана половине произв-я катетов. Пусть АВ=АС=х. S=49


, то есть

см.
Ответ:

см, 49 см^2.